Calculator is probably the most important thing you can have with you during the entrance examination. Wise use of calculator enables you to solve most questions in least time. This blog is about how you can use CASIO fx-991ES for your best benefit, but is may prove equally important for the users of other models too. Almost all of the 25 Mathematics questions (40 marks) can be solved in very little time by using calculator, and this time can be allocated to other questions.

Before everything, make sure you know the location of each keys. The following image of 991ES PLUS is used in the entirety of this blog:

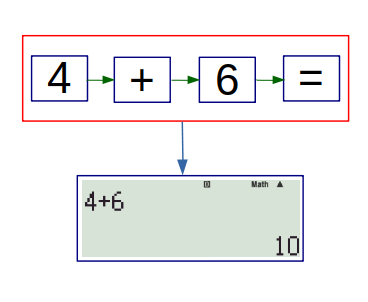
The processes of calculation are shown by the use of flowcharts in this blog. In the flowcharts, red rectangles are for ‘input’ (which keys to press and in what order) and blue are for ‘output’ (what result you should expect in the display). The order in which the keys should be pressed is indicated by green arrows. For example, the following flowchart shows how you can add 4 and 6.

 

 

Setting Up the Calculator

 

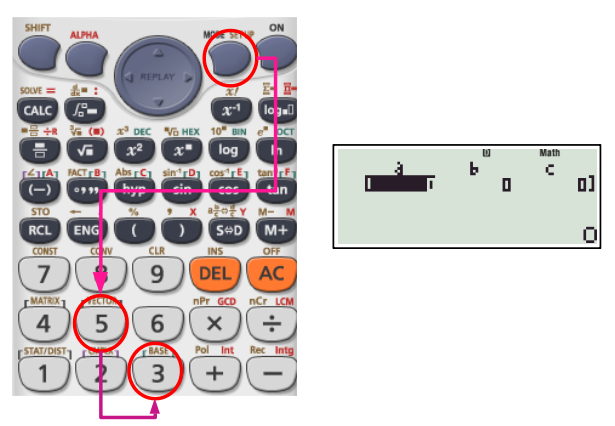
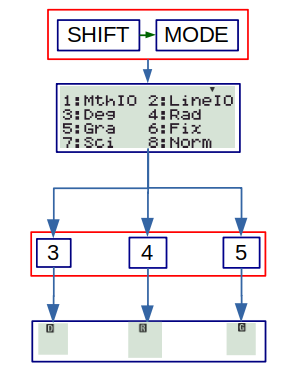
Once the calculator is ON, you can go to SETUP menu by pressing SHIFT key and then MODE key. There are different options for changing units of angle (discussed later), and format of number display. There is even an option to adjust the contrast. These options should be changed whenever necessary. For example, if you want the result to be in scientific notation, you should activate ‘SCI’, (option 7), and similarly, if you want to see just 3 digits after decimal, activate ‘FIX’ and type ‘3’. You can change the result between fraction and decimal by pressing the ‘S-D’ key. Pressing SHIFT and then ‘S-D’ key allows conversion to and from mixed fractions. You may want to play with these simple operations before moving forward.

 

There are two different prints above almost all keys. The pink print represents what is typed when the key is pressed after pressing the ALPHA key. Similarly, the brown print represents what is typed when the key is pressed after pressing the SHIFT key. When SHIFT and ALPHA keys are pressed, a small indicator ‘S’ and ‘A’ are shown on the top left corner of screen respectively.

 

Calculator Compatible Chapters

 

This section deals with some specific chapters of Mathematics, whose questions are specifically solved by calculator. An example is also provided for each chapter.

 

Sequence and Series:

 

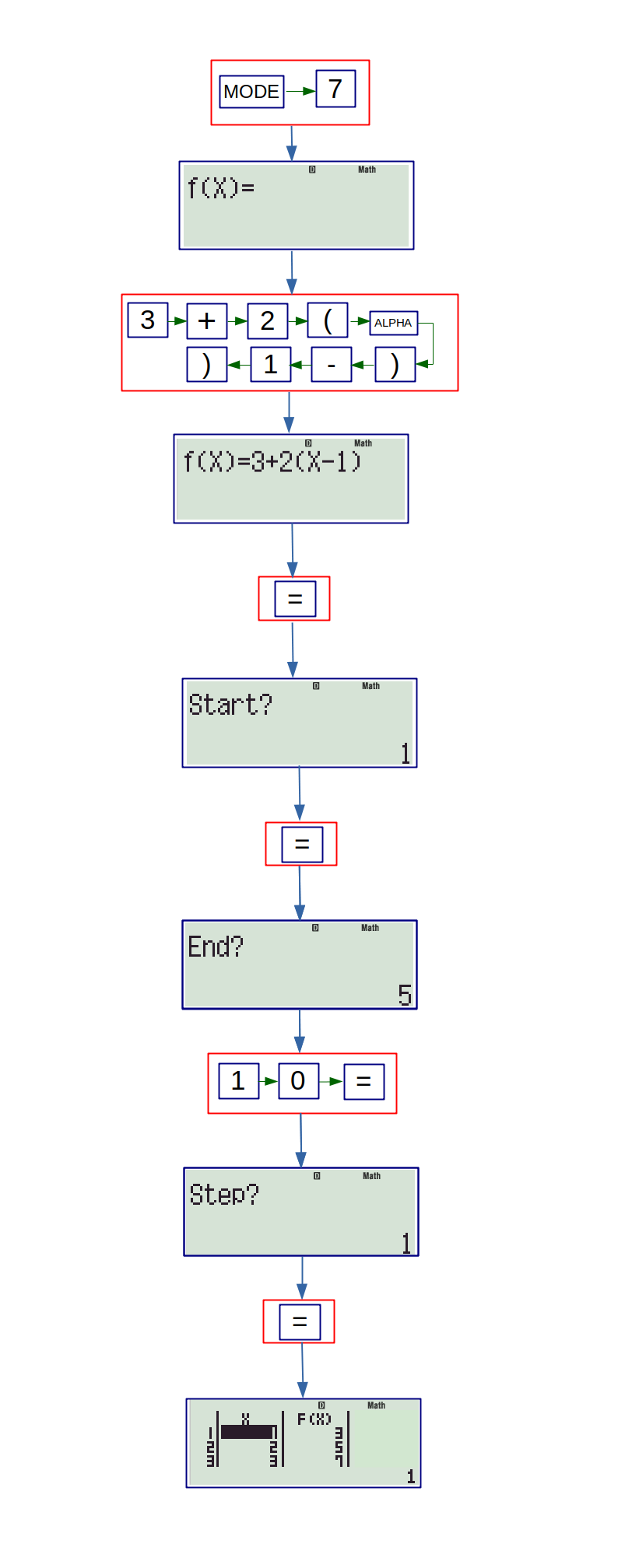
Different sequences can be generated using the TABLE mode. This mode can be activated by pressing following keys in the order indicated.

 

 

For this, we model the sequence as a function of \(x\), and assume \(x\) to represent order of number in the sequence. For example, an AP with common difference \(2\) starting with \(3\) will be modeled as:

\( f(x) = 3 + 2(x – 1) \)

which is just an alternative notation to \( t_n = a + d(n-1) \)

 

The following flowchart shows how to generate above sequence for 1^st to 10^th terms.

 

 

Now, using the navigation keys (the big circle) you can see all terms of the sequence.

Similarly, other sequences can be generated and studied.

 

Example: If second term of a GP is 4 times the third term and the first term is 2 more than second term, the 4^th term of the sequence is:

 

(a) \(1/4\)

(b) \(-1/4 \)

(c) \(1/4! \)

(d) none of these

 

Let the sequence be \(a, ar, ar^2, ar^3 \)

By given;

\( ar = 4ar^2 \Rightarrow r = \cfrac{1}{4} \)

Similarly, \( a = 2 + a/4 \Rightarrow a = \cfrac{8}{3} \)

 

Now, using the TABLE mode, we generate this sequence, using function,

\( f(x) = \cfrac{8}{3} \left( \cfrac{1}{4} \right)^{x-1} \)

 

 

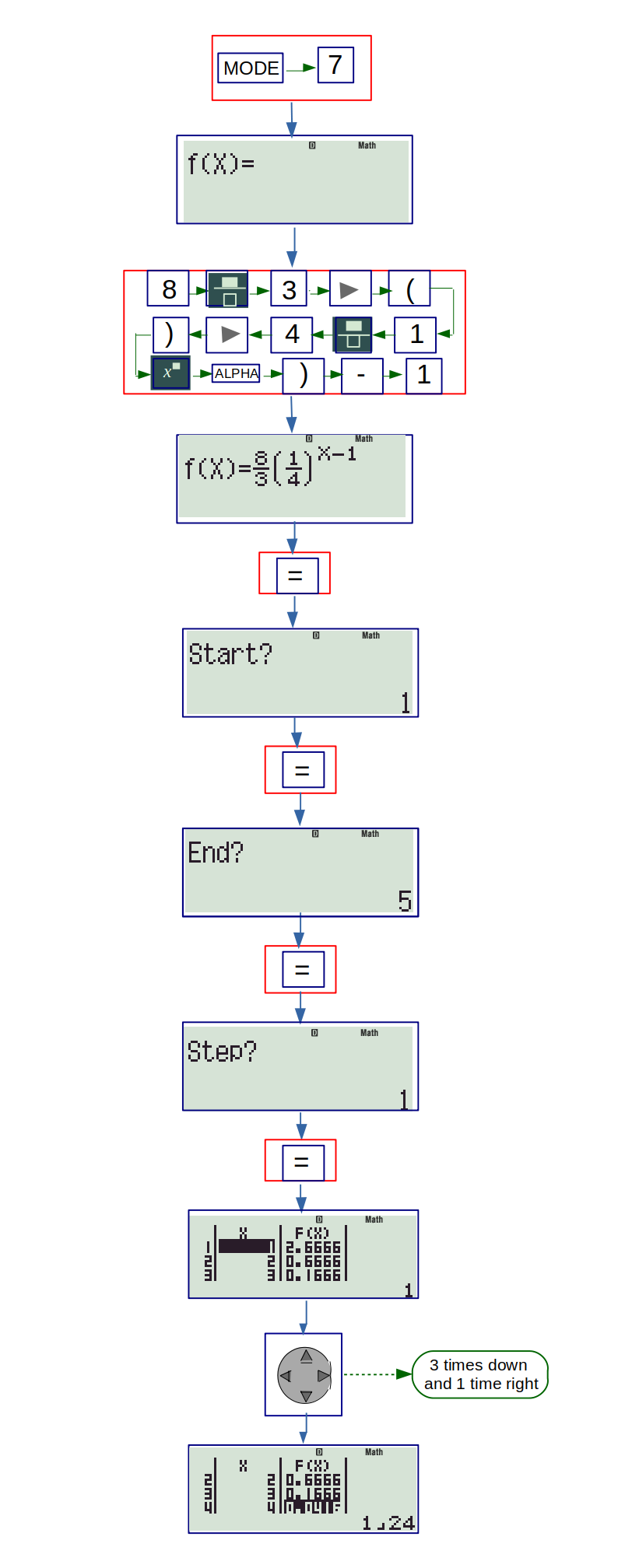
The calculator shows fourth number to be \(1/24 = 1/4! \)

 

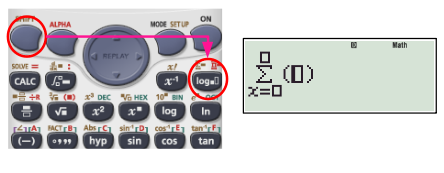
A more useful feature is the SUMMATION, equivalent to any series. The sigma notation is displayed once the corresponding key is pressed. The function to be summed is typed and then the limits are given.

 

 

Example: If sum of all terms of a sequence \( 3,5,9,17,…\) is 1031, the number of terms in the sequence is:

(a) 7

(b) 8

(c) 9

(d) 10

 

Note that, the general term is \( t_n = 2^n + 1 \).

So, the value of \(A\) that satisfies:

\( \displaystyle{\sum_{x=1}^{A} (2^X + 1) = 1031} \)

is the answer.

 

The following flowchart shows how to check for option (a). Using CALC, we can check for other options too.

 

 

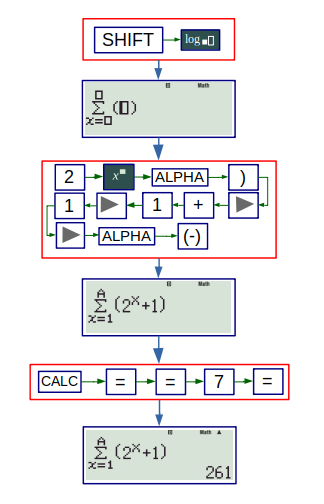
Trying this out for different values of A gives correct answer. (c)

You don’t need to repeat the whole process. Just press CALC again.

 

Polynomial Equations:

 

Quadratic equations can be solved very easily (even cubic equations) with 991ES. There is a separate mode, EQUATIONS for this. Besides the polynomial equations, it also allows one to solve simultaneous linear equations. This section deals with quadratic equations only.

 

The quadratic equation \(ax^2 + bx + c = 0 \) is solved in EQN mode:

 

 

Example: If the roots of \(2x^2 + 3x - 8 = 0 \) and \( x^2 + 3x - a \) are in the ratio 1:2, then \(a=\)

 

(a) 14

(b) 16

(c) -16

(d) -14

 

Using calculator we solve \( 2x^2 + 3x - 8 = 0 \),

 

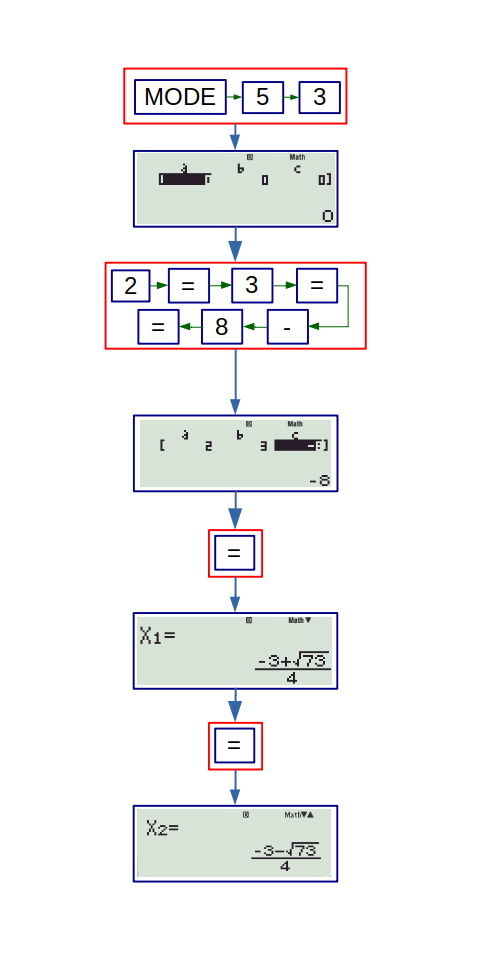
So, by question, the roots of unknown equations are:

\( \cfrac{-3 + \sqrt{73}}{2}, \cfrac{-3 - \sqrt{73}}{2} \)

 

Solving the equations for different values of \(a\), we get the correct answer, (b).

 

Trigonometric and Hyperbolic functions:

 

991ES supports operations on trigonometric, inverse trigonometric, hyperbolic and inverse hyperbolic functions.

 

 

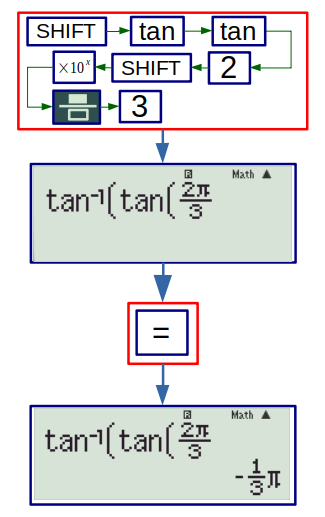
The inverse trigonometric functions are typed once the SHIFT key is pressed followed by the respective key of trigonometric function.

 

While working with these functions, it is almost always necessary to keep angles in radian. The small ‘D’, ‘R’ or ‘G’ indicated whether the angles are measured in degrees, radians or grades.

 

To change the units, the following procedure is to be followed:

 

 

Example: \( \tan^{-1} (\tan (2 \pi/3)) = \)

 

(a) \(2 \pi/3 \)

(b) \( \pi / 3 \)

(c) \( -\pi / 3 \)

(d) \( \sqrt{3} \)

 

First make sure, the angles are in radian. (‘R’ on top of screen, not ‘D’, not ‘G’). Then, the answer is obtained easily as:

 

 

In the upcoming flowcharts, the details to type a function or an expression is not given. It is expected for you to learn how to type any expression by now.

 

 

Permutation and Combination: These are trivial calculations involving factorials. Just the keys are indicated below:

 

 

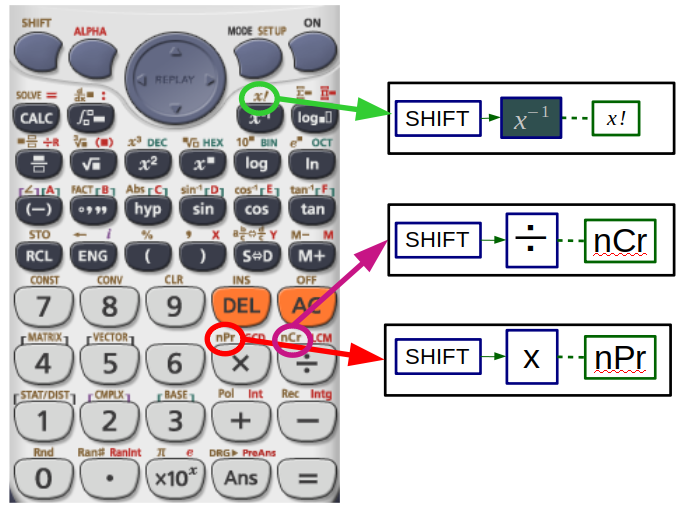
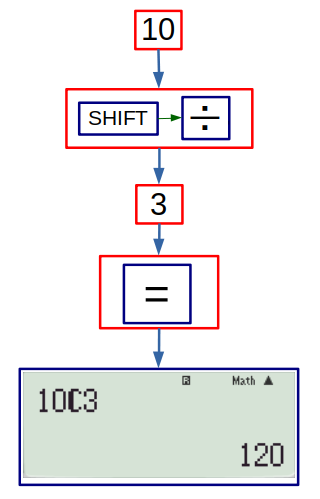
The syntax for \( {}^nC_r \) is \(nCr\) and for \( {}^nP_r \) is \(nPr\).

So, to find \( {}^10C_3 \) the following flowchart is adopted:

 

 

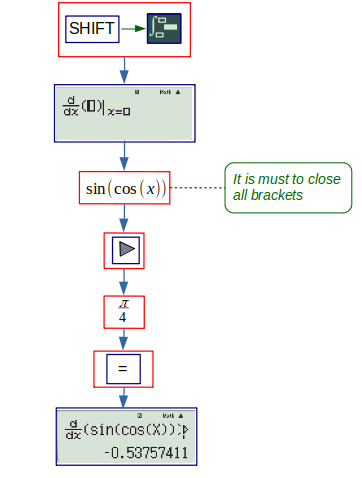
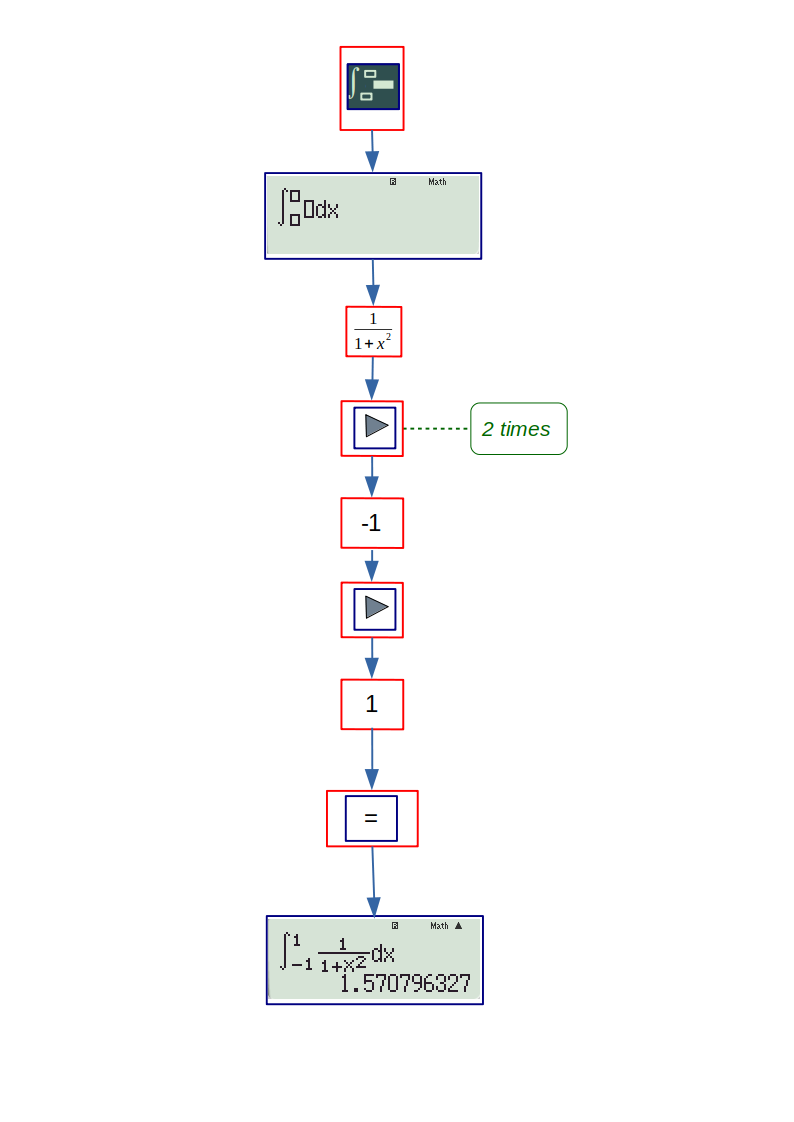
Derivatives and Integration: Although 991ES allows evaluation of definite differentiation and integration, it can be used to perform indefinite operations, when options are available. The flowcharts for evaluating definite integrals and derivatives are given below. The integration, \( \displaystyle {\int_{-1}^{1} \left( \cfrac{1}{x^2 + 1} \right) dx} \) and derivative of \( \sin(\cos x) \) at \( x = \pi/4 \) are evaluated in the flowcharts.

 

(a) derivative:

 

 

(b) integration:

 

 

The following two examples illustrate how we can use this approach to evaluate indefinite operations.

 

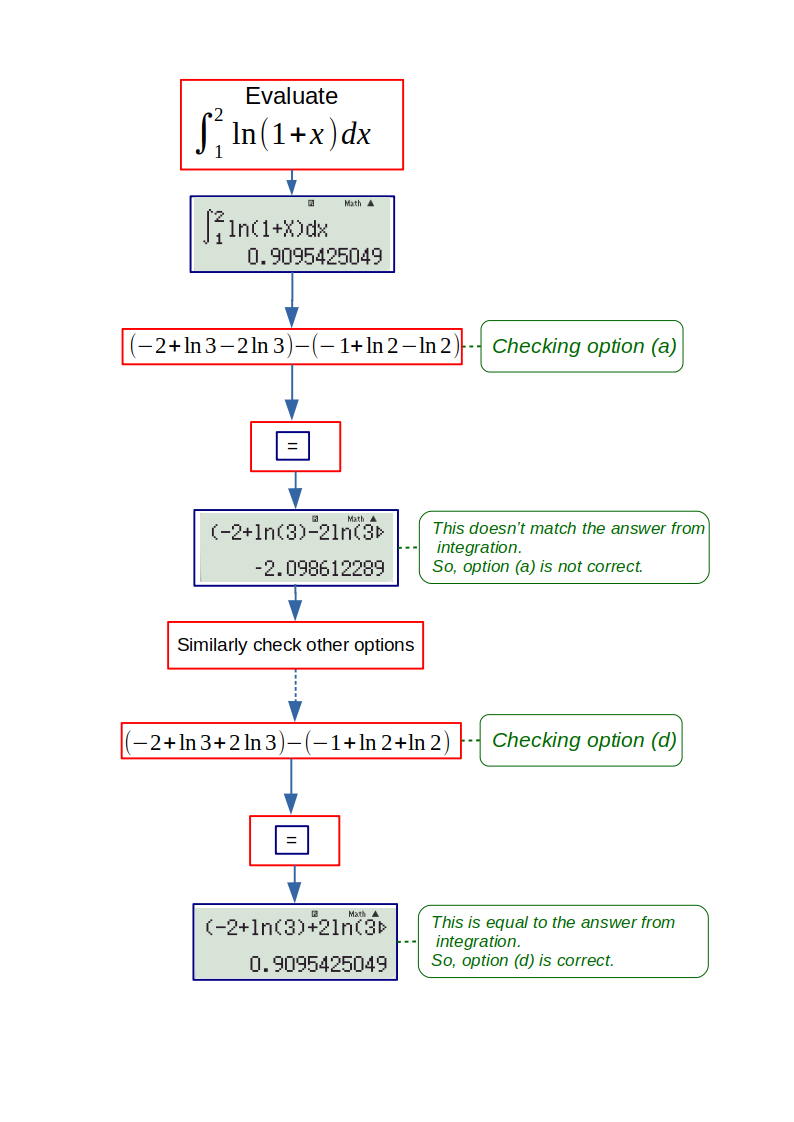
Example: \( \displaystyle{\int \ln(1+x) dx = } \)

 

(a) \(-x + \ln(1+x) – x \ln (1+x) \)

(b) \(-x - \ln(1+x) – x \ln (1+x) \)

(c) \(-x - \ln(1+x) + x \ln (1+x) \)

(d) \(-x + \ln(1+x) + x \ln (1+x) \)

 

To check which option is correct, we evaluate the integral with arbitrary limits (that are in the domain of the function to be integrated), say ‘a’ to ‘b’. Then for each function in the options we evaluate \( F(b) – F(a) \). By fundamental theorem of calculus, the two answers should be equal.

 

For this question, \( a = 1 \), \(b=2\) is chosen.

 

 

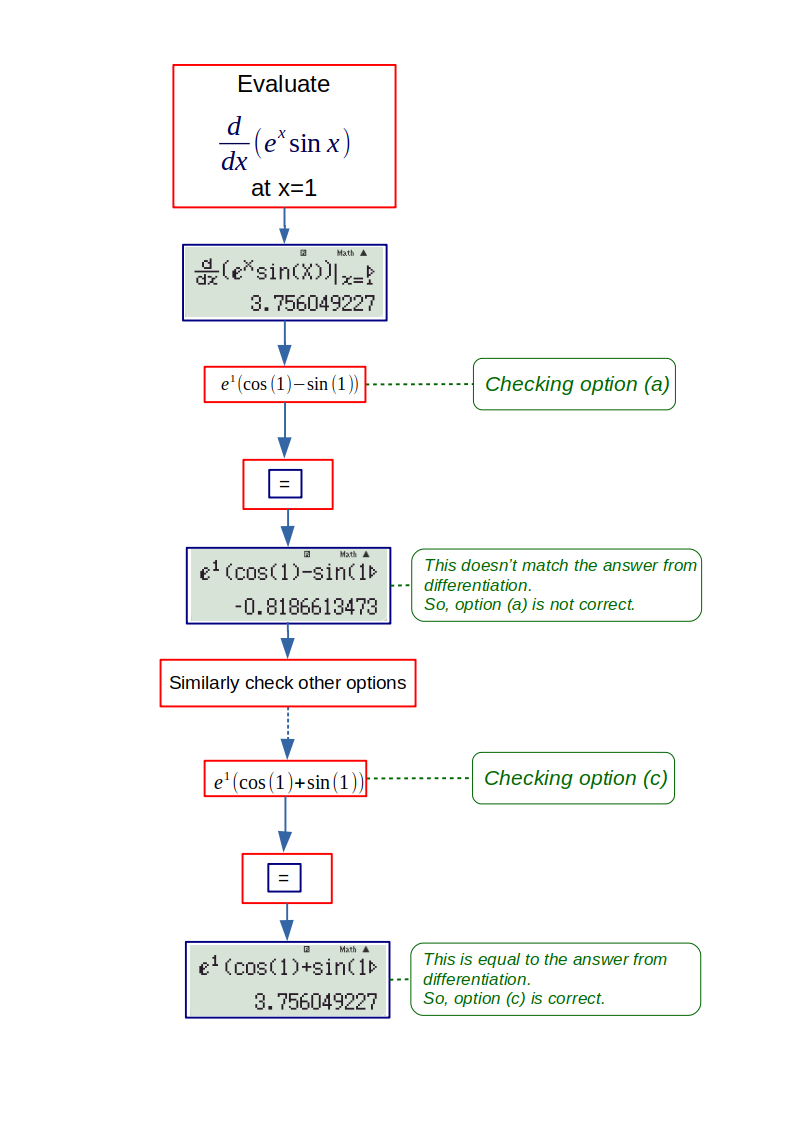
Example: \( \cfrac{d}{dx} (e^x \sin x) = \)

 

(a) \(e^x(\cos x - \sin x) \)

(b) \(e^x(-\cos x + \sin x) \)

(c) \(e^x(\cos x + \sin x) \)

(d) \(-e^x(\cos x + \sin x) \)

 

To check which option is correct, we evaluate the derivative at any value of x (say a). Then for each option we evaluate \( f(a) \). The two answers should match.

 

For this question, \(x=1\) is chosen.

 

Since we are working with radian angles, make sure the calculator’s units are proper. (R indication on the screen)

 

 

 

Modes

 

Next, we see some chapters with dedicated modes. They are vectors, complex numbers and matrix and determinants. The number in parenthesis given in title of each mode represents their order in the MODE menu. Once the MODE key is pressed, and then the indicated number key is pressed, the mode is activated. When a mode is activated, an indication is displayed on the top of screen. The indications are tabulated below:

 

SN	Mode	Indication
1	COMP	Math
2	COMPLX	COMPLX
3	STAT	STAT
4	BASE-N	-
5	EQN	-
6	MATRIX	MAT
7	TABLE	-
8	VECTOR	VCT

 

 

The first mode is for general computations, and is not described.

 

COMPLX mode (2) :

 

This mode is for calculations involving complex numbers. The imaginary unit can be typed by pressing ENG key. The option menu is displayed by pressing SHIFT followed by ‘2’. The required option is activated by pressing the numeric keys shown.

 

 

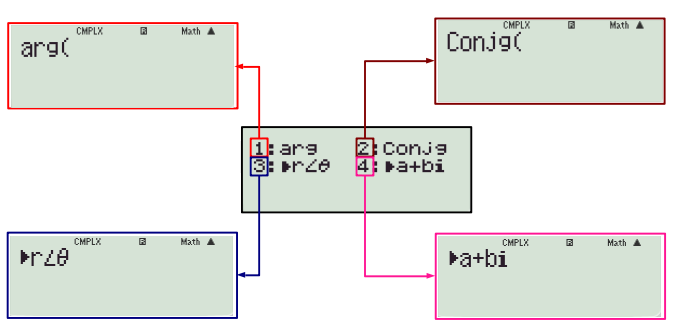
Options:

 

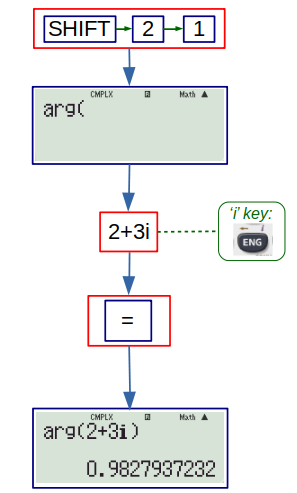
1. arg: This is used to calculate argument (or amplitude ) of a complex number. For instance, the argument of \( 2+3i \) can be found as follows:

 

 

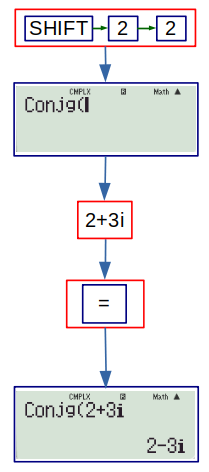
2. Conjg: Conjugate of a complex number. The conjugate of a complex number \( a+ib \) is \( a – ib \). The conjugate of \( 2 + 3i \) can be found as follows:

 

 

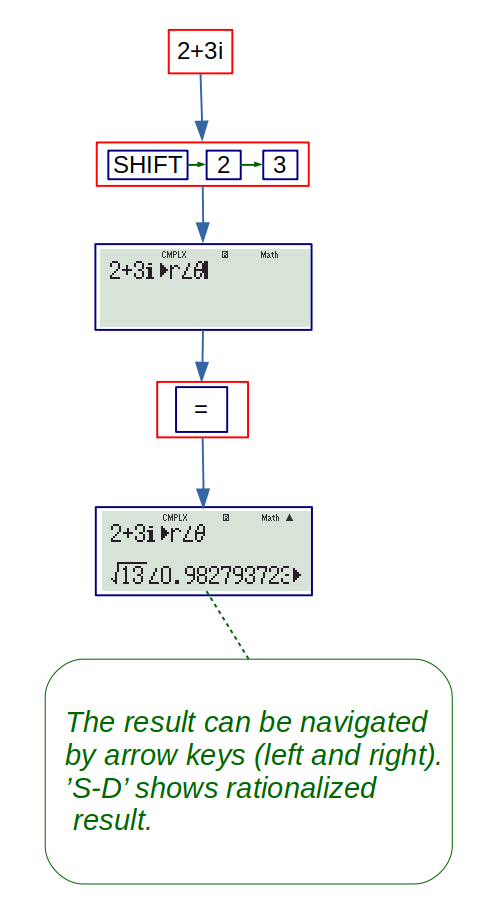
3. \(r \angle \theta \): To convert cartesian representation to polar representation. The polar representation of \( r(\cos \theta + i\sin \theta) \) is given as \( r \angle \theta \). The polar form of \( 2 + 3i \) is found as follows:

 

 

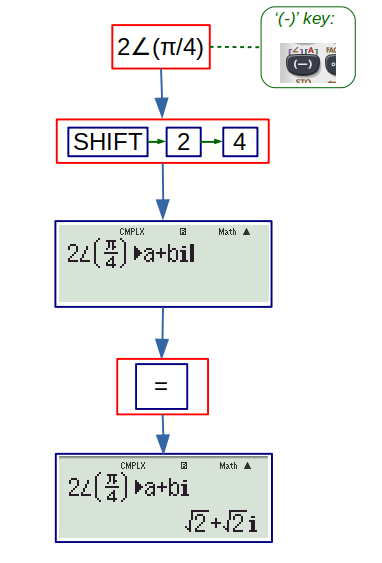
4. \( a + ib \) : To convert polar representation to cartesian representation. To type \( r \angle \theta \), the angle is typed by pressing SHIFT followed by the ‘(-)’ key. The polar form \( 2 \angle \pi/4 \) is converted to cartesian form as follows:

 

 

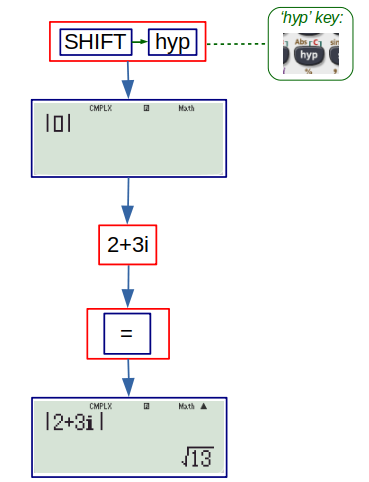
The modulus of a complex number, and vectors too can be found (similar to the real numbers) by using the ‘Abs’ key. For instance, the modulus of \( 2+3i\) can be found as follows:

 

 

Example: The modulus of \( \cfrac{1-i}{1+i} \) is:

 

(a) \(1\)

(b) \(-1\)

(c) \(i\)

(d) none of these

 

 

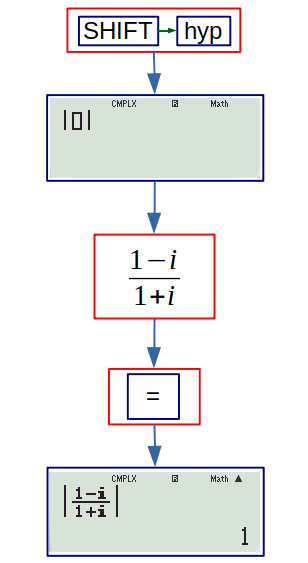
From the entrance point of view, the STAT mode is not necessary, (Statistics is not in the syllabus).

 

BASE-N deals with conversion and computation in different number bases, and is described at the end.

 

EQN mode (5): This is perhaps the most important mode, as simultaneous linear equations and polynomial equations occur unexpectedly in various problems. Solving polynomials is already discussed, and now we focus on simultaneous equations.

 

The options of equation mode are displayed once the mode is activated. As per the form of equations, the correct option is chosen.

 

SN	Option	Purpose
1	anX + bnY = cn	Linear equations in 2 variables
2	anX + bnY + cnZ = dn	Linear equations in 3 variables
3	aX2 + bX + c = 0	Quadratic equation
4	aX3 + bX2 + cX + d=0	Cubic equation

 

The following flowchart depict procedure for solving two simultaneous equations:

\( 2x + 4y = 10 \\ 4x – 3y = 5 \)

 

 

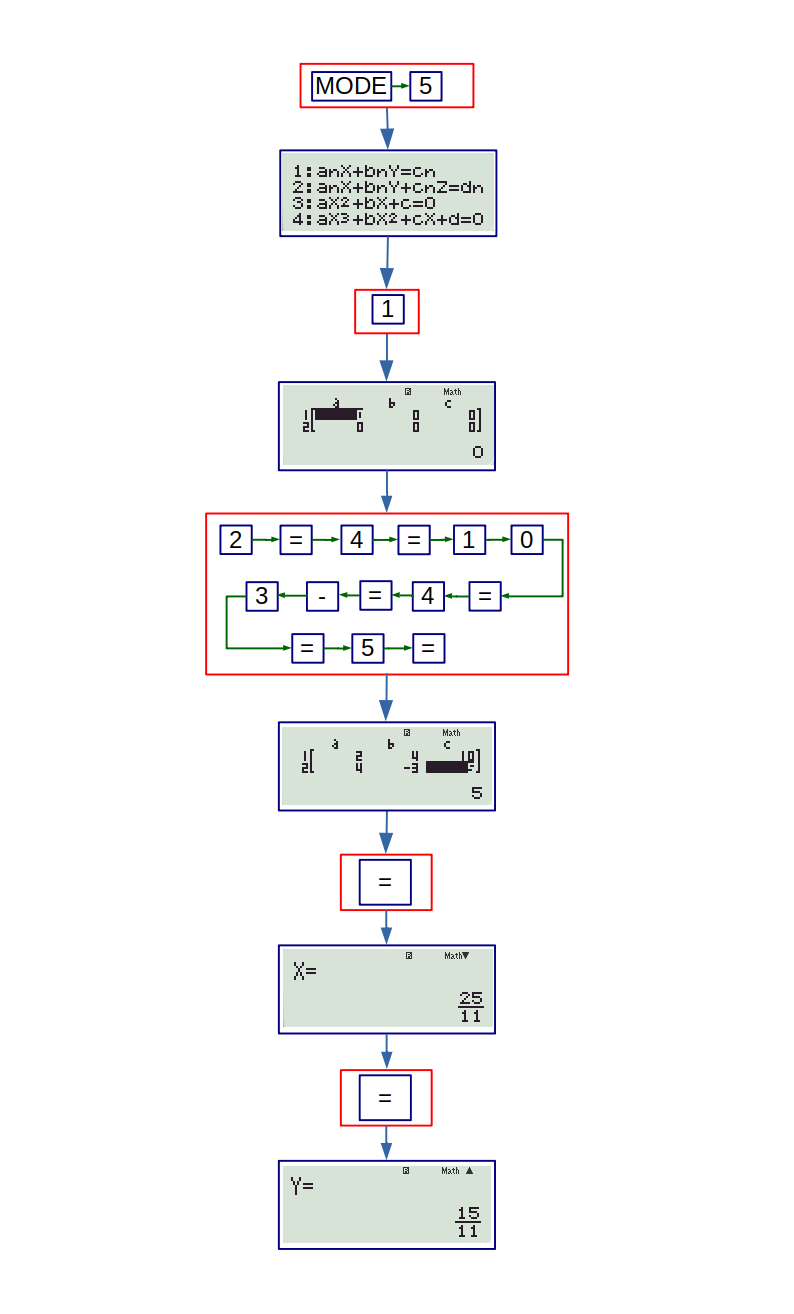
The following flowchart depict procedure for solving three simultaneous equations:

\( 2x + 3y – 5z = 10 \\ 3x – 4y + 2z = 8 \\ 2x – 4y + 7z = -3 \)

 

 

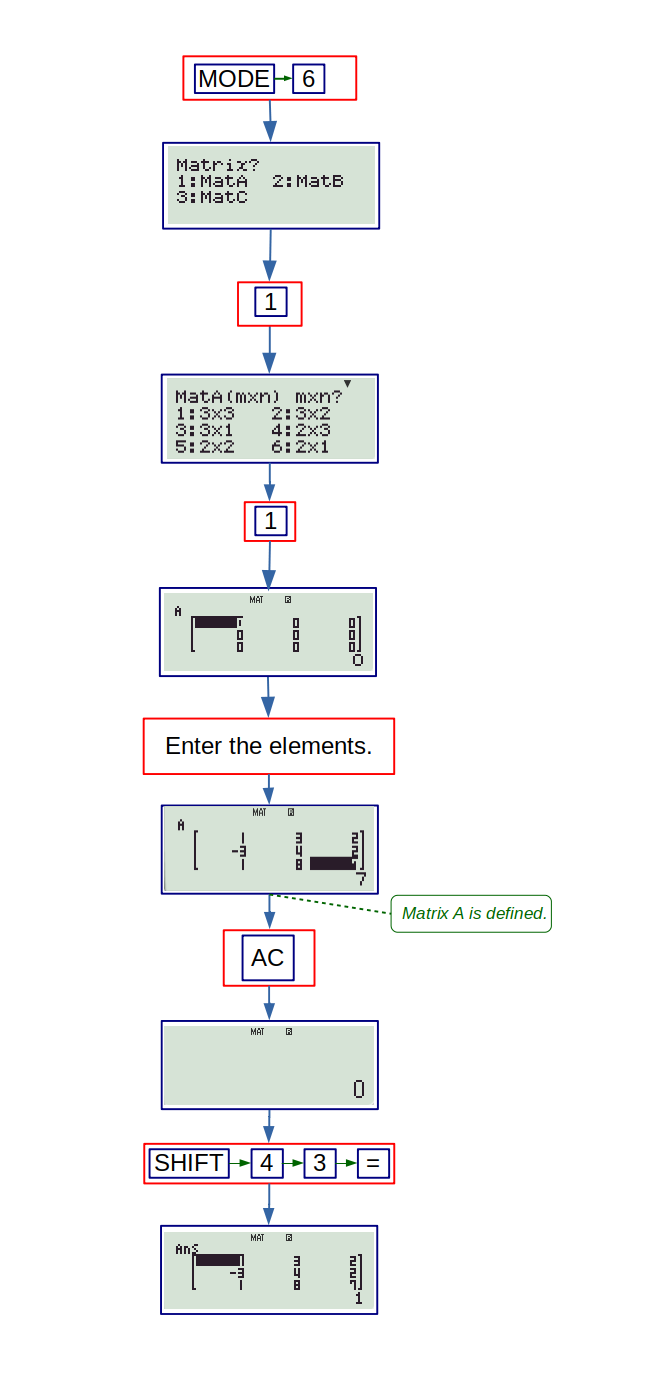
MATRIX mode (6): The matrix mode is dedicated to solve problems related to matrix and determinants. 991ES supports matrices with at most 3 rows and columns. The option menu is displayed by pressing SHIFT key followed by numeric 4 key. Before performing any calculations, it is necessary to input data for different matrices, at most 3. These matrices are named A, B and C. Once the matrices are well-defined they can be accessed and edited from the option menu. The following flowchart shows how to define the given matrix and access it:

\( \left[ \begin{matrix} 1 & 3 & 2 \\ -3 & 4 & 2 \\ 1 & 8 & 7 \end{matrix} \right] \)

 

The matrices can also be defined later from option menu. The various options are described below. First make sure that your calculator in in MATRIX mode.

It is not compulsory to define a matrix once MATRIX mode is active. You can skip it by pressing ‘AC’ key.

 

Options:

1. Dim: It is used to define a matrix. The following flowchart shows how to define a new matrix (or redefine existing one) using this option:

 

 

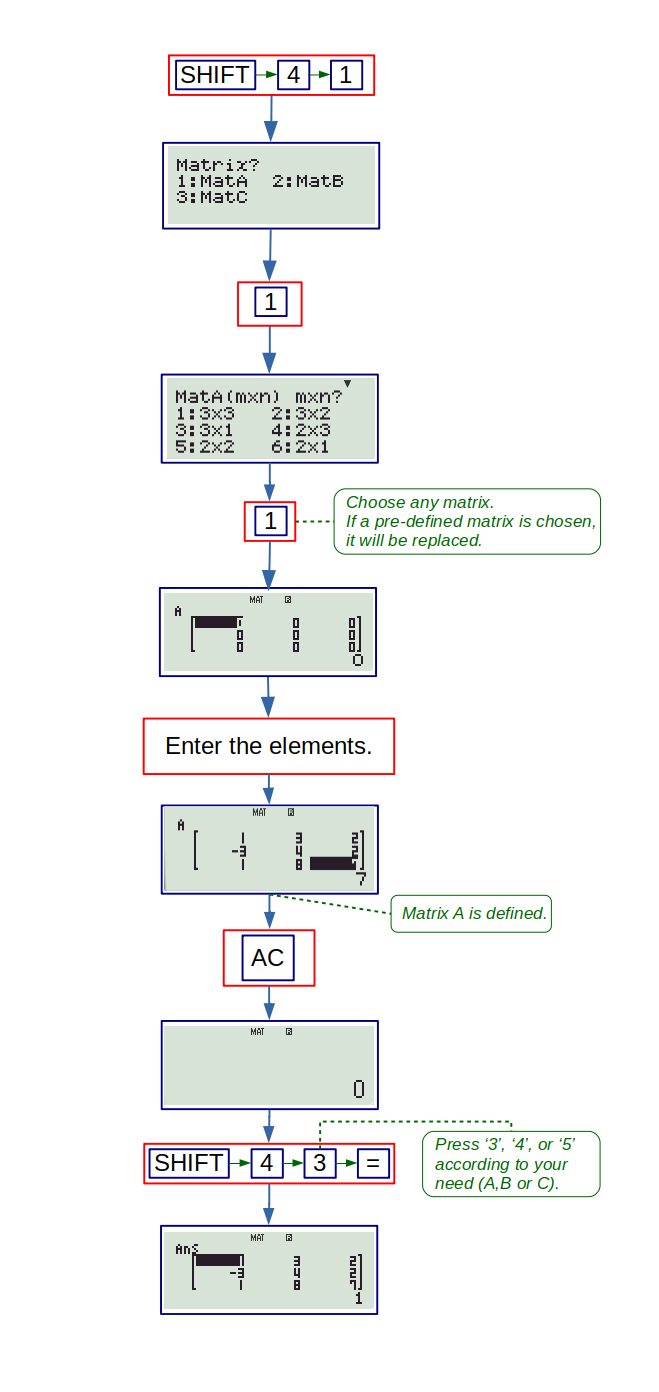
2. Data: It is also like ‘Dim’ but the order (or dimensions) of the matrices can’t be changed if they are already defined. So, this option is suitable for editing elements of a pre-defined matrix. The following flowchart shows how to edit elements of a pre-defined matrix using this option:

 

 

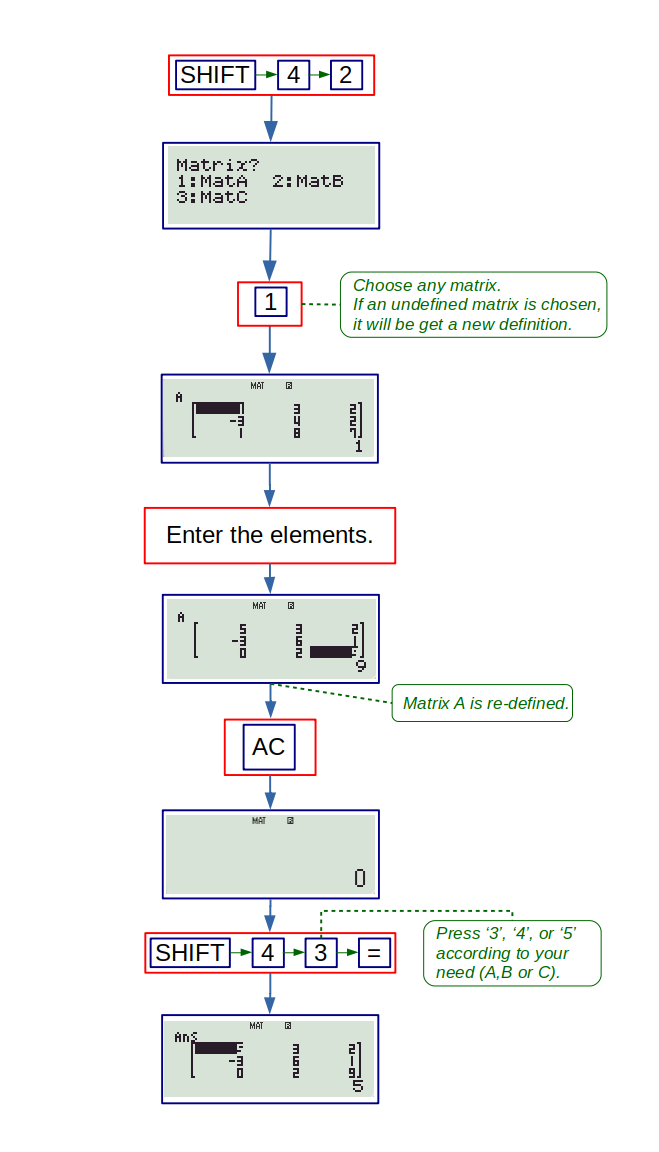
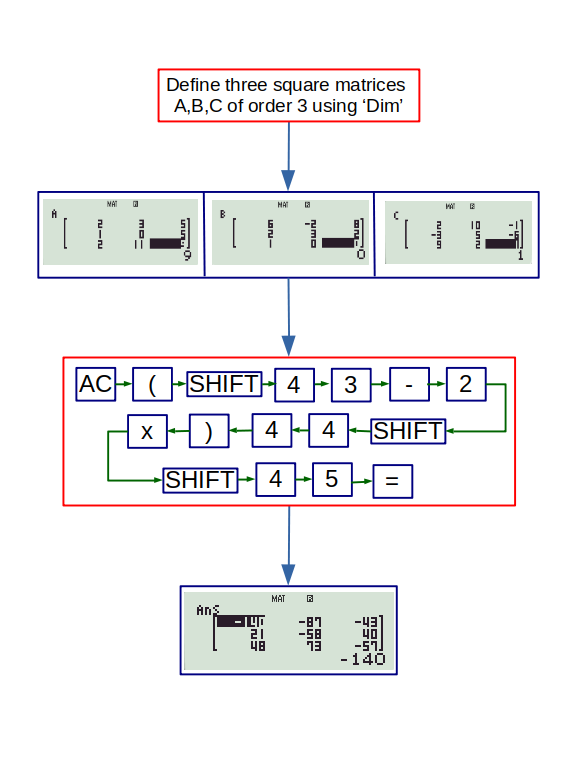
3,4,5,6: These options are to access the matrices and perform other calculations. Ordinary ‘+’, ‘-’, ‘x’ keys work for matrix operations too. The option ‘MatAns’ is for accessing the last matrix given by the calculator. For instance, if you perform \( A+B \) and then want to find \( 3(A+B) \), you can simply do 3(MatAns). The following flowchart shows how to perform \( (A – 2B) \times C \) for three square matrices of order 3.

 

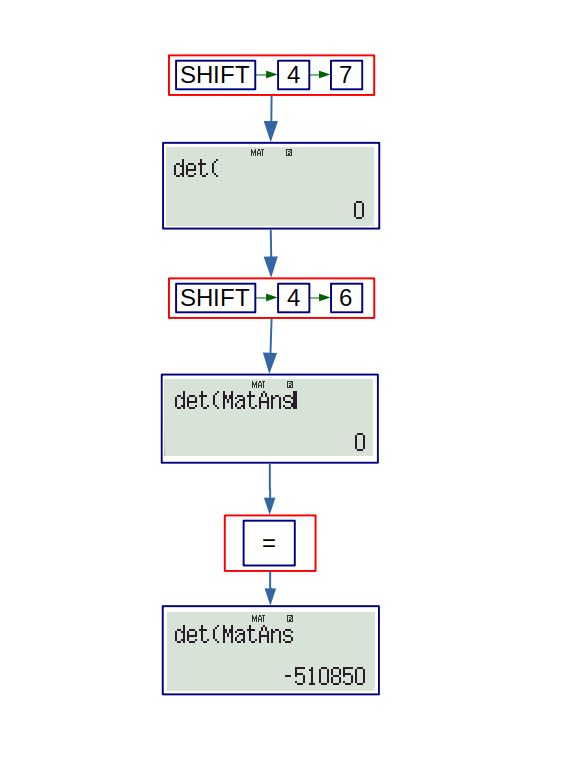
7. det: This option is to find determinant of the matrices. The following flowchart shows how to find determinant of the last matrix answer.

 

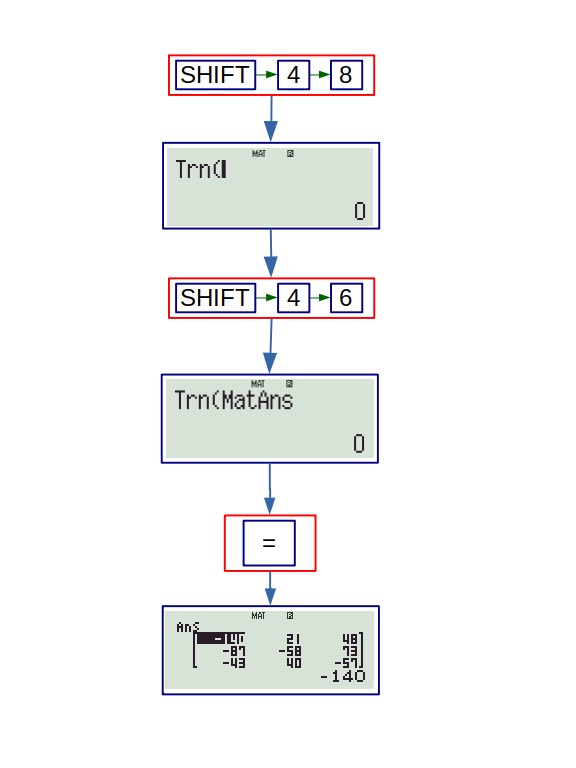
8. Trn: This option is to find transpose of the matrices. The following flowchart shows how to find transpose of the last matrix answer.

 

Example: If \(A = \begin{bmatrix} 0&0&0 \\ 0 & 0 & 0 \\ 1 & 0 & 0 \end{bmatrix}\) then:

 

(a) \(A^2=A\)

(b) \(A^3=A\)

(c) \(A^2=-A\)

(d) none of these

 

First we define the matrix A, and find its powers. Then we can easily see which option is correct.

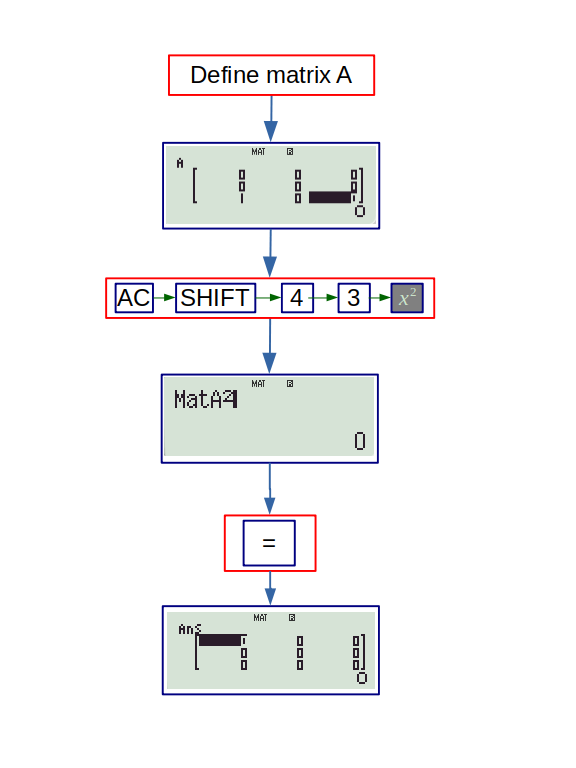
Since the square of A is null matrix, all its higher powers will also be null. So, (d) is correct.

 

Although the square key (and the cube) works good with matrices, you can’t use the power key. Instead, you will have to continue the product.

 

Example: If \(x=2\) is a root of \( \begin{vmatrix} x-a & 1 & 2 \\ 0 & x^2 & 1 \\ 1 & 2 & 3 \end{vmatrix} = 0 \), then \(a=\)

 

(a) 11/10

(b) 12/10

(c) 13/10

(d) none of these

 

If \(x=2\) is root of the given equation,

\(\begin{vmatrix} 2-a & 1 & 2 \\ 0 & 4 & 1 \\ 1 & 2 & 3 \end{vmatrix} = 0 \)

 

We define the matrix for different values of ‘a’, from options, and that value which gives 0 is correct. It is a good exercise to do it on your own.

 

The inverse of matrix can be found by using the inverse key. The flowchart to find inverse of matrix A is:

 

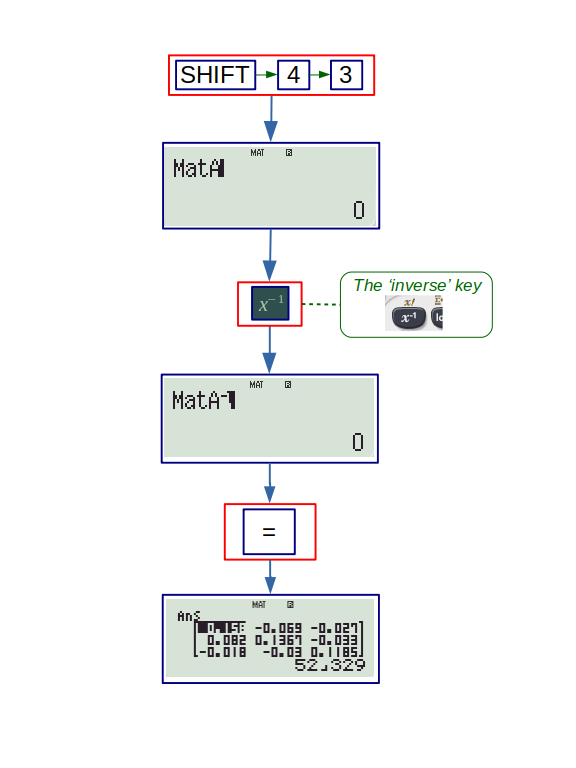
The TABLE mode is already introduced under ‘sequence and series’. It will be further discussed later.

 

VECTOR mode (8): The vector mode is dedicated to vectors as the name suggests. The options ‘Dim’ and ‘Data’ are similar to the matrix mode. There is option for dot product, and the ordinary ‘x’ sign represents cross product.

 

Example: For a unit vector \(\vec{a}\), the expression \( | \vec{a} \times \hat{i} |^2 + | \vec{a} \times \hat{j} |^2 + | \vec{a} \times \hat{k} |^2 \) evaluates to:

 

(a) 0

(b) 1

(c) 2

(d) 3

 

We can assume \(\vec{a} \) to be any unit vector. For instance let \( \vec{a} = \hat{i} \). Then we just need to replace \(\vec{a}\) with \(\hat{i}\) and see the result.

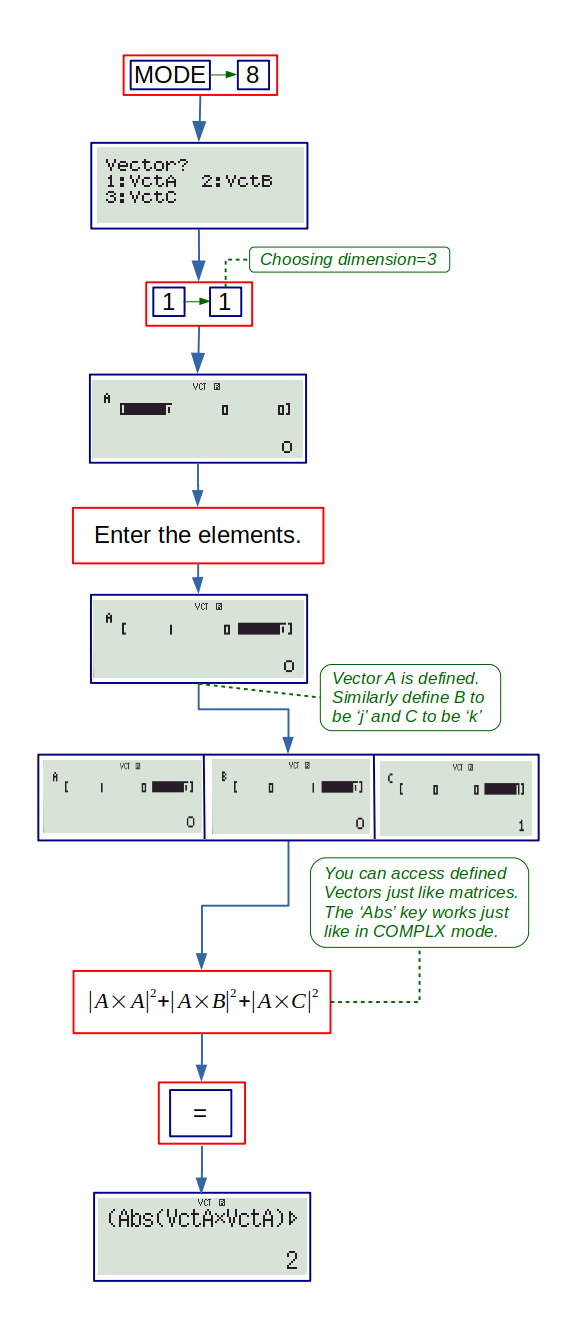
What more?

 

The previous sections were focused on straightforward calculations and were like guidelines for using the calculator. On the basis of the discussion so far, now we proceed towards less-obvious computations. For this purpose, we use the memory of calculator in form of ‘variables’. We will also use TABLE mode to perform some operations like finding domain and range, evaluating limits and solving trigonometric equations.

 

SOLVE:

 

When we have a complex equation with a single variable, 991ES can solve the equation provided that we provide the initial guess wisely. We solve the equation with ‘SOLVE’ activated by pressing CALC key after pressing SHIFT key.

 

The following flowchart shows how to solve \( e^x = 3\sin x \) with this function.

 

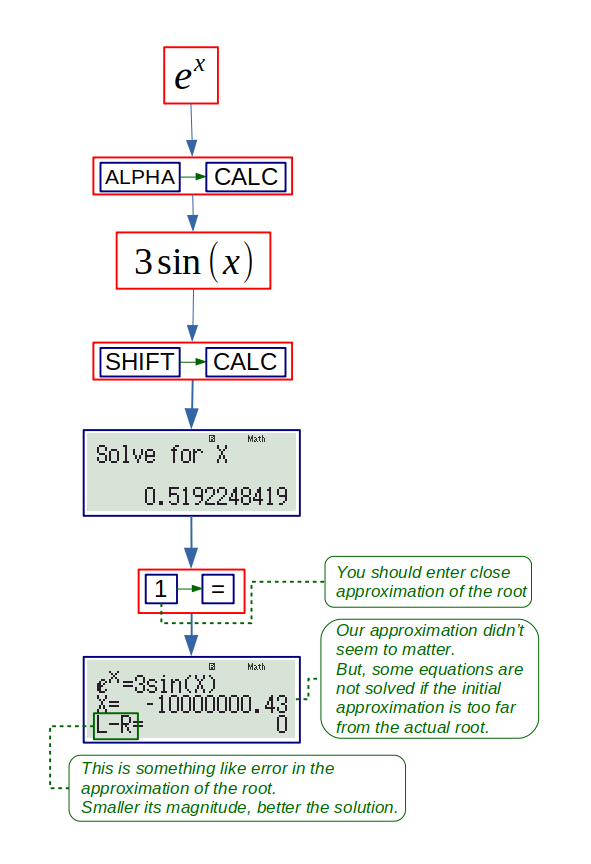
Example: The point of intersection of \( y = x^2 \) and \(y=2x-1\) is:

 

(a) \( (1,1) \)

(b) \( (-1,1) \)

(c) \( (-1,-1) \)

(d) none of these

 

If \(x=a\) is intersection, then \( a^2 = 2a-1 \). Solving \( x^2 = 2x-1 \), we get from calculator \(x=1\), and \(y=x^2 \) gives \(y=1\). So, \((1,1)\) is the point of intersection.

 

What would be two points of intersections if the line was \(y=2x+1\) ?

 

The TABLE mode:

 

I hope you remember how to generate a sequence using the TABLE mode. Using that knowledge, we are going to find domain and range of functions, and also solve trigonometric equations.

 

Example: The range of the function \( f(x) = \sqrt{x^2-2x+5} \) is:

 

(a) \( [ -2 , \infty) \)

(b) \( [2, \infty) \)

(c) \( (-\infty, 2] \)

(d) none of these

 

Using the TABLE mode, we can generate the sequence for \( f(x) \) with convenient limits and steps. (Note that the memory is limited!).

 

For this question, we can choose the limit from -10 to 10 with step 1.

 

Observing the values, the range can be found as \( [2, \infty) \).

 

The minimum value is obtained at point of symmetry (vertex), which is at \(x=1\) since the value of \(f(x)\) goes on increasing equally when ‘x’ increases or decreases from this point.

 

Example: The domain of \( f(x) = \ln (1-x^2) \) is:

 

(a) \( (-\infty,0] \)

(b) \( [0, \infty) \)

(c) \( [-1,1] \)

(d) \( (-1,1) \)

 

To find domain of the given function, generate the function’s sequence in the interval defined in the options, with suitable intervals.

 

For this question, for option (a), start from -10, end to 0, with step 1. The function will be defined only at \(x=0\). So, this is discarded. For, option (b), start from 0, end to 10, with step 1. Once again, the function is only defined at 0. So, this is also discarded. For option (c) start from -1, end to 1, with step 0.1. This clearly shows that option (d) is correct.

 

Example: The most general value of \( \theta \) satisfying \( \sin \theta + \cos \theta = 1 \) is:

 

(a) \( 2n \pi \pm \cfrac{\pi}{4 }\)

(b) \( n \pi + (-1)^n \cfrac{\pi}{4} - \cfrac{\pi}{4} \)

(c) \(2n \pi \)

(d) \( (4n+1) \cfrac{\pi}{4} \)

 

Next, generate the sequence for \(\theta\) using the function given in options. The option giving most general values is correct.

 

For this question, option (a) should be resolved into two parts, one for positive and other for negative sign. The interval’s limits can be \( [0,2\pi] \) with step \( \pi/4 \). Further, it is suggested to factor out \(\pi\) and then generate the sequence.

 

The following flowchart shows the sequence generated for option (a), keeping the minus sign.

 

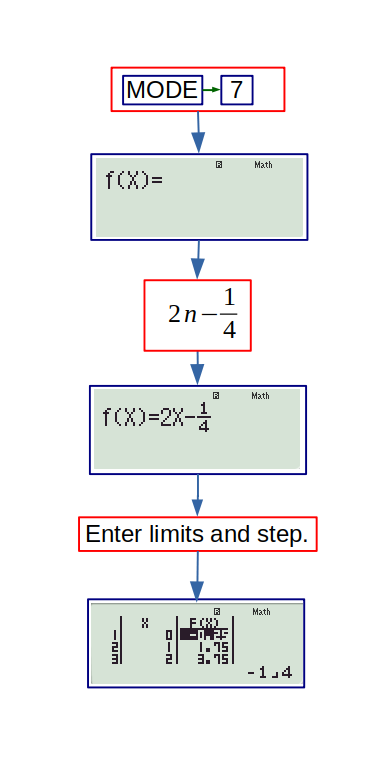
Similarly, considering \(+\) sign too, the sequence can be written as: \( -1/4,1/4,7/4,9/4 ,... \) Note that, the values given by this sequence doesn't satisfy our equation. So, it is discarded.

The most general sequence giving valid angles only, is \(0,1/2, 2,... \), generated from option (b). So, this is correct answer.

 

BASE-N mode:

 

This mode allows conversion and calculations in different number bases. After it is active (MODE no 4), the base is indicated just above the output answer. The keys for changing the bases are serially arranged in the second row of the black keys’ pad.

 

 

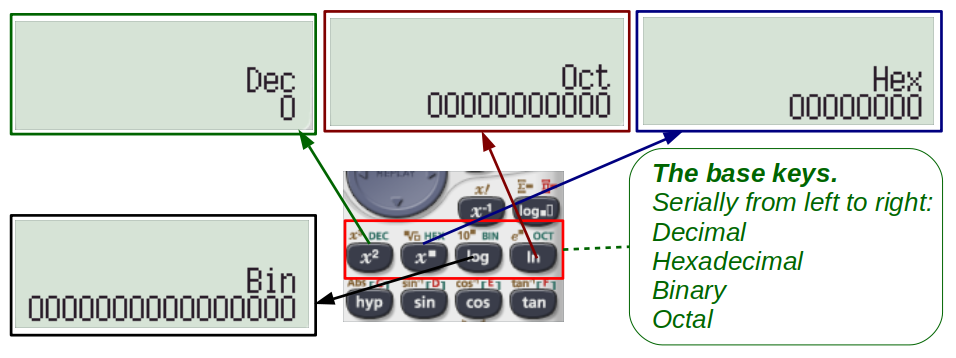
When a number is typed in one base, and key of any other base is pressed, the conversion is automatically done. The calculations can be done similar to normal calculations, without changing the base.

 

Conversion and Constants:

 

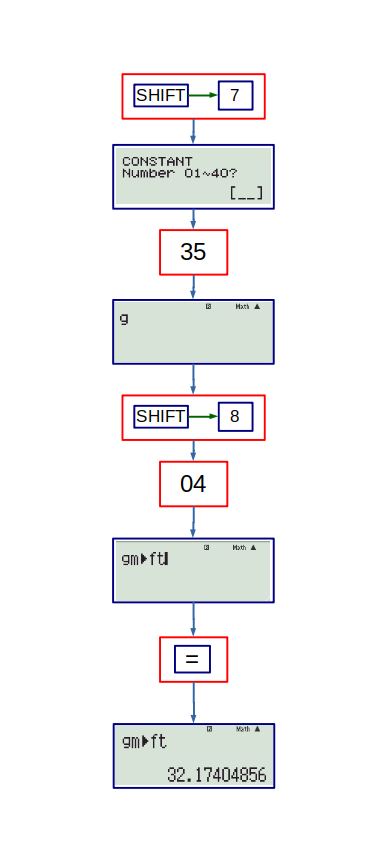
These features are important in solving some problems of physics, and even chemistry. After pressing the SHIFT key, and then numeric 7, the option to enter a ‘constant number’ appears. There are 40 different constants for forty different numbers. (Printed on the inside of back cover) These can be accessed and manipulated as necessary.

 

Similarly, on pressing the SHIFT key and then numeric 8, conversion menu is displayed. To use the conversion ‘a>b’, the units of ‘a’ should be typed first, and then the proper conversion should be selected form the menu, and then ‘=’ should be pressed. For, instance, the following flowchart shows how to convert the acceleration due to gravity (in \(m/s^2\) ) to \( ft/s^2 \):

And at last…

 

Should you always use the calculator? Actually, no. Since using calculator can save you time (and space), you should consider learning the basics. However, sometimes using calculator can cost you even more time. Further, using calculator DOESN’T mean, you have to study less. To know how the methods work, and use them by really understanding when to use, requires even deeper study. Also, combining the basics of what you have learned so far, I suggest you to develop whatever short-cuts you desire. And the most important of all, NEVER rely on a method you don’t understand. Better slow and safe than fast and dead!