Mathematics

1. Trissecting an Angle
   
   1. Consider an angle \(\angle AOB\) to be trisected.
      
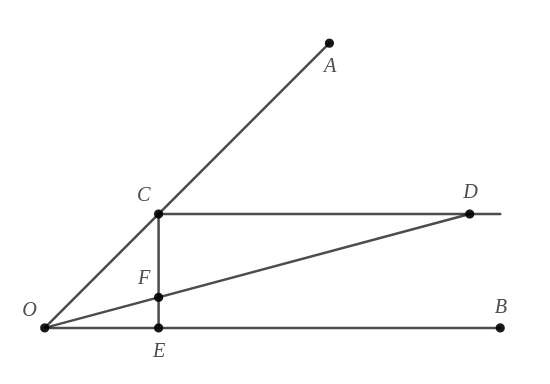
      \(CE\) is drawn normal to \(OB\) and \(CD\) is drawn parallel to \(OB\). Let \(OC=x,FD=y, \angle AOD= \theta , \angle DOB= \alpha\).
      Express \(CF , FE\) and \(CE\) in terms of \(x,y, \alpha\) and \(\theta\).
   2. Using results from (a) derive
      \[ \cfrac{\sin(\alpha+\theta)}{\sin (\alpha)} - \cfrac{\cos(\alpha+\theta)}{\cos(\theta)} = \cfrac{y}{x} \quad (1) \]
   3. Simplify the LHS of equation (1) to prove
      \[y=\cfrac{2\sin(\theta)}{\sin(2\alpha)}x\quad(2)\]
   4. Devise a suitable method to trisect \(\angle AOB \) using a marked straightedge and compasses based on equation (2).
      (This method is actually used in engineering drawing.)
      
      Solution:
      In \(\Delta CFD\,\, CF = FD \sin \alpha\)
      In \(\Delta EFO\,\, FE = OE \tan \alpha\)
      In \(\Delta OCE\,\, OE = OC \cos (\alpha+\theta)\)
      and \(CE = OC \sin (\alpha+\theta)\)
      
      Combining all these relations and since \(FD=y, Oc=x\)
      
      \(CF = y \sin \alpha \\ FE = x \cos (\alpha+\theta)\tan\alpha \\ CE = x \sin (\alpha+\theta)\)
      
      Also, \( CE = CF + FE\)
      
      \(x \sin(\alpha+\theta) = y \sin \alpha + x \cos(\alpha+\theta)\tan \alpha \\ \cfrac{y}{x}=\cfrac{\sin(\alpha+\theta)-\cos(\alpha+\theta)\tan\alpha}{\sin \alpha} \\ \cfrac{y}{x} = \cfrac{\sin(\alpha+\theta)}{\sin \alpha} - \cfrac{\cos(\alpha+\theta)}{\cos \alpha}\)
      
      Simplifying LHS,
      \(\begin{align} \cfrac{\sin(\alpha+\theta)}{\sin \alpha} - \cfrac{\cos(\alpha+\theta)}{\cos \alpha} &= \cfrac{\sin(\alpha+\theta)\cos \alpha - \cos(\alpha+\theta)\sin \alpha}{\sin \alpha \cos \alpha} \\ &= \cfrac{\sin(\alpha+\theta-\alpha}{\sin \alpha \cos \alpha} \\ &= \cfrac{2 \sin \theta}{\sin 2 \alpha} \end{align}\)
      
      So,
      \(y = \cfrac{2 \sin \theta}{\sin 2 \alpha} x\)
      
      To trissect the angle, it is desirable to have \(\alpha = \theta/2 \Rightarrow \theta=2\alpha\)
      
      Then equation (2) gives \(y=2x\).
      
      Based on this the procedure to trissect angle \(\angle AOB\) is:
      
      1. Draw \(CE\) and \(CD\) arbitratily.
      2. With one end fixed at \(O\) rotate the marked straightedge. noting the distance \(FD\) until \(FD=2\times CO\)
      3. Join \(OFD\)
2. The Heron's Problem
   
   1. The following figure depicts a popular problem in Mathematics called the “Heron's Problem”. A farmer at A wants to carry water from river \(XY\) to the well \(W\). If he can travel in straight lines only and \(AW \parallel XY\), we want to find the shortest possible path.
      
      
      
      
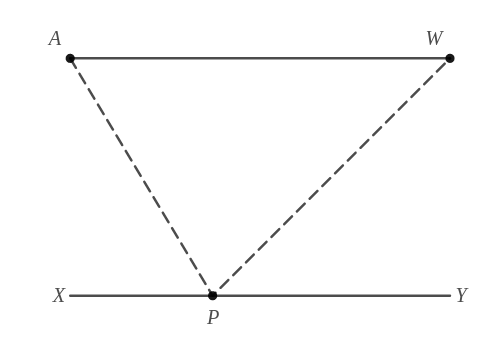
      Let \(X\) be the origin, and \(AX \perp XY\) so that \(AXY\) forms a Cartesian frame. Assume \(AW=l\) (the distance from farmer to well) and \(AX=h\) (the distance from farmer to the river).
      If the distance the farmer has to travel is denoted by \(s\) (shown by dashed line), express \(s\) as a function of \(XP=x\) and \(h\) only.
      Compute \(\cfrac{ds}{dx}\) and hence prove that if \(APW\) is the required solution, \(AP=PW\).
      (Substitute \(y=l-x\))
   2. Compute \(\cfrac{d^2 s}{d x^2}\) and hence prove that if \(AP=PW\), \(APW\) is the required solution.
      
      
   3. Solving the problem by calculus is computationally difficult. We will now solve the same problem geometrically.
      The following figure shows some additional constructions. \(A'\) and \(W'\) are reflections of \(A\) and \(W\) about the line \(XY\) respectively. \(APW\) and \(AP''W\) are two possible paths. \(AP'W\) is a path such that \(AP'=P'W\).
      
      
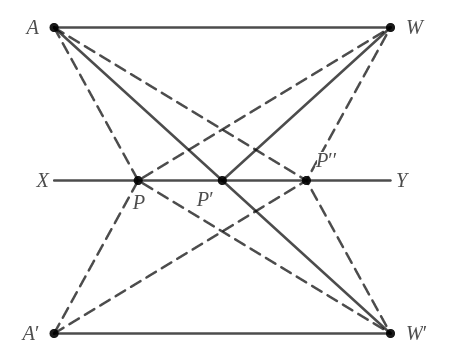
      Prove that \(AP'W'\) is a straight line.
      
      
   4. Considering that \(XY\) serves as line of reflection, prove that \(APW' , AP'W'\) and \(AP''W'\) are equal in distance to the paths \(APW\), \(AP'W\) and \(AP''W\) respectively.
      Using triangle inequality in \(\Delta APW'\) and \(\Delta AP''W'\) prove that \(AP'W\) is shortest among the three paths.
      Argue that \(AP'W\) is the shortest path possible.
      
      Solution:
      
      Since there is nothing special about the point \(Y\), assuming \(WY \perp XY\) doesn't affect the problem.
      
      By given:
      \(XP = x \\ PY = l-x \\ AX = WY=h\)
      And, using Pythagorean theorem,
      \(s = \sqrt{x^2+h^2}+\sqrt{(l-x)^2+h^2}\)
      
      Also let \(y=l-x\)
      so that \(\cfrac{dy}{dx}=-1\)
      
      With the use of chain rule, we can compute the first derivative:
      
      \(\cfrac{ds}{dx} = \cfrac{1}{2} (x^2+h^2)^{-1/2} \times 2x - \cfrac{1}{2} (y^2+h^2)^{-1/2} \times 2y\)
      
      If \(APW\) is required path, \(s\) should be either minima or maxima. So,
      
      \(\cfrac{ds}{dx}=0\)
      
      This gives,
      \(\cfrac{x}{\sqrt{x^2+h^2}}=\cfrac{y}{\sqrt{y^2+h^2}} \\ \Rightarrow \cfrac{x^2}{x^2+h^2}=\cfrac{y^2}{y^2+h^2} \\ \Rightarrow \cfrac{x^2+h^2}{x^2} = \cfrac{y^2+h^2}{y^2} \\ \Rightarrow \cfrac{h^2}{x^2} = \cfrac{h^2}{y^2} \\ \Rightarrow x=y\)
      
      This is sufficient to prove \(AP=PW\).
      
      For the second part, we should prove \(\cfrac{d^2 s}{dx^2} >0\)
      
      Using the quotient rule,
      \(\cfrac{d^2s}{dx^2} = \cfrac{\sqrt{x^2+h^2}-\cfrac{x^2}{\sqrt{x^2+h^2}} }{x^2+h^2} + \cfrac{\sqrt{y^2+h^2}-\cfrac{y^2}{\sqrt{y^2+h^2}} }{y^2+h^2}\)
      
      After some simplification,
      \(\cfrac{d^2s}{dx^2} = \cfrac{h^2}{(x^2+h^2)^{3/2}} + \cfrac{h^2}{(y^2+h^2)^{3/2}} > 0\)
      
      Hence the proof.
      
      For the geometrical proof:
      
      Since \(XY\) is axis of reflection, \(PW=PW', P'W=P'W', P''W=P''W''\)
      
      It is obvious that \(\angle AWW'=90^\circ\)
      Further, \(AP=PW=PW'\)
      
      So, if a circle of radius \(AP\) is drawn with center at \(P\), an inscribed angle of \(90^\circ\) is formed at \(W\). This is enough to conclude that \(APW'\) is diameter and hence a straight line.
      
      Due to reflective symmetry \(APW = APW', AP'W=AP'W'\) and \(AP''W=AP''W'\)
      
      Using triangle inequality in two triangles stated by question,
      
      \(AP+PW' > AP'W' \\ AP'' + P''W' > AP'W'\)
      
      Since there is nothing special about \(P\) and \(P''\), the proof is enough to generalize for all paths left and right from \(P'\).
      Hence \(AP'W\) is the shortest path possible.
      
      
3. Focusing with a Parabola
   
   1. Consider a parabola \(y^2 =4x\) as shown in figure below. A ray \(y=c\) strikes the parabola at \(P\). This is reflected such that the normal is angular bisector of incident ray and reflected ray as shown in the figure.
      (The incident ray is \(AP\) and the reflected one is \(PS\).)
      
      
      
      

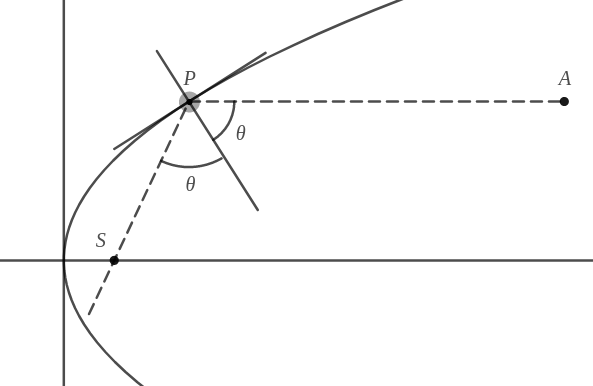
      Find the slope of normal at point \(P\).

      (In terms of \(c\) )
   2. If \(m_ 1\) be the slope of normal and \(m_ 2\) be that of reflected ray, derive a relation between \(m_ 1\) and \(m_ 2 \).
      
      
   3. Find \(m_ 2\) and hence equation of the reflected ray.
      
      
   4. Note that, \(S\) is the point on axis of symmetry of the parabola. Prove that it is the focus.
      So, any ray incident to the parabola parallel to the axis of symmetry is reflected through its focus. This principle is used in parabolic reflectors.
      
      Solution:
      
      Equation of parabola is \(y^2=4x\)
      
      The incident ray is \(y=c\)
      
      Coordinates of \(P\) can be computed as \( \left( \cfrac{c^2}{4},c \right) \)
      [Put \(y=c\) and find the value of \(x\)]
      
      The slope of normal is:
      
      \(m = \cfrac{-1}{dy/dx} = -\cfrac{dx}{dy}\)
      
      \(x = \cfrac{y^2}{4} \\ \cfrac{dx}{dy} = \cfrac{y}{2} \)
      
      So the slope of normal at \(P\) is \(-c/2\).
      
      Let \(\theta_1\) and \(\theta_2\) be angle made by normal and reflected ray with incident ray (or X-axis) respectively.
      
      So, \(m_1 = \tan \theta_1 \,\, m_2 = \tan \theta_2\)
      
      Also, \(\theta_1 = 180^\circ - \theta\)
      \(\theta_2 = 180^\circ - 2 \theta\)
      
      Combining these two relations
      
      \( 2\theta_1 = \theta_2 + 180^\circ \\ \Rightarrow \tan(2\theta_1) = \tan \theta_2 \\ \Rightarrow \cfrac{2m_1}{1-m_1^2} = m_2 \\ \Rightarrow m_2 = \cfrac{2m_1}{1-m_1^2} \)
      
      Also, \(m_1 = -c/2\)
      
      So, \(m_2 = \cfrac{4c}{c^2-4}\)
      
      The reflected ray has slope \(m_2\) and passes through \(P=(c^2/4,c)\). With this information, the equation of reflectef ray is:
      
      \(y = \cfrac{4cx}{c^2-4}+c-\cfrac{c^3}{c^2-4}\)
      
      Put \(y=0\) for the axis of symmetry,
      
      \(0 = \cfrac{4cx}{c^2-4} + c - \cfrac{c^3}{c^2-4} \\ \Rightarrow 4cx + c(c^2-4) - c^3 = 0 \\ \Rightarrow 4cx + c^3 -4c - c^3 = 0 \\ \Rightarrow x=1\)
      
      So, the reflected ray passes through the focus \(S(1,0)\) which completes the proof.

Physics

1. Rocket Dynamics
   
   
   1. A rocket of mass \(M\) is about to be launched from a stationary platform in space at \(t=0\) s. The rocket is designed to release its fuel at a constant rate of \(\dot{m}=\cfrac{d m}{d t}(\mathrm{kg} \text { per second })\) with velocity \(u\) relative to the rocket. If the rocket travels in a straight line, neglecting all external forces (i.e. force of gravity and drag), express velocity of rocket as a function of its mass (\(m\)) present at the moment.
      
      Solution: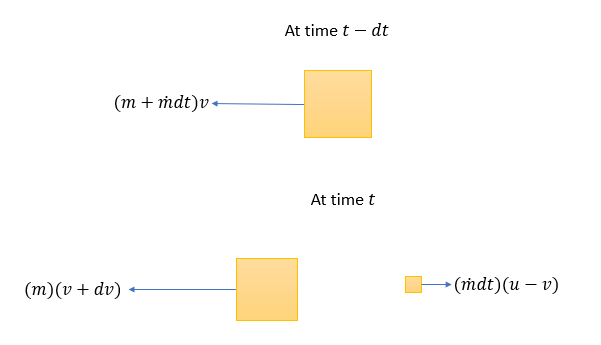
      
      Using conservation of linear momentum in absence of forces,
      \(m(v+dv)-(\dot{m}dt)(u-v)=(m+\dot{m}dt)v\)
      \(\Rightarrow mdv=\dot{m}dtu\)
      \(\Rightarrow mdv=-dmu [\dot{m}dt=-dm \text{ i.e. mass lost by rocket at time dt }]\)
      \(\Rightarrow \displaystyle \int_0^v dv=-u\displaystyle \int_M^m\cfrac{dm}{m}\)
      \(\Rightarrow v=u\ln\left(\cfrac{M}{m}\right)\)
      
      
   2. Express the distance travelled by the rocket as the function of its mass \((m)\).
      
      Solution:
      From (a), \(\cfrac{ds}{dt}=u\ln\left(\cfrac{M}{m}\right)\) .....(i) Here mass of rocket \(m\) is variable, so we cannot integrate over time.
      From \(\dot{m}dt=-dm \Rightarrow dt=\cfrac{-dm}{\dot{m}}\)
      Substituting \(dt\) in (i) and integrating, we get,
      \(\displaystyle \int_0^s ds=\cfrac{u}{\dot{m}}\displaystyle \int_M^m\ln\left(\cfrac{m}{M}\right)dm\)
      \(\Rightarrow s=\cfrac{u}{\dot{m}}\left|m\ln\left(\cfrac{m}{M}\right)-m\right|_M^m\)
      \(\Rightarrow s=\cfrac{u}{\dot{m}}\left[(M-m)+m\ln\left(\cfrac{m}{M}\right)\right]\)
      
      
   3. Taking the initial mass and rate of release of fuel of rocket to be \(500 \text{ tones}\) and \(100 \mathrm{ kg}\) per second respectively, calculate the mass of propellent and energy required for the rocket to attain a velocity of \(50,000 \mathrm{km} / \mathrm{hr} .\) The rocket releases fuel at velocity of \(2000 \mathrm{m} / \mathrm{s}\) relative to itself.
      
      Solution:
      From (a), mass of rocket when it attains velocity \(v\) is given by the equation
      \(m=Me^{-\cfrac{v}{u}}\)
      Given \(v=50000 \mathrm{km} / \mathrm{hr}=13888.8 \mathrm{m} / \mathrm{s}, u=2000 \mathrm{m} / \mathrm{s}, M=5\times 10^5 \mathrm{kg}\),
      
      Mass of rocket at velocity \(13888 \mathrm{m} / \mathrm{s} = 5\times 10^5 \times e^{-\cfrac{13888.8}{2000}}=482 \mathrm{kg}\)
      \(\therefore\) Mass of propellent \(=5\times 10^5-482=499518 \, \mathrm{kg}\)
      
      Total energy required = Kinetic energy of rocket mass left + Sum of Kinetic energy of fuel released over the journey
      \(=\cfrac{1}{2}\times m_f \times v_f^2+\displaystyle \int_0^{499518}\cfrac{1}{2}dm(v-u)^2\)
      \(=\cfrac{1}{2}\times 482\times 13888.8^2 + \cfrac{1}{2} \times 2000^2 \displaystyle \int_0^499518 \left(\ln\left(\cfrac{5\times 10^5}{m}\right)-1\right)^2dm\)
      \(=1.0455\times 10^{12} \, J\)
      
      
   4. Calculate the time taken by the rocket to travel a distance of \(0.1 \mathrm{AU}\) if the rocket stop burning its fuel at velocity \(50,000 \mathrm{km} / \mathrm{hr}\).
      
      Solution:
      Distance travelled by the rocket before it attains velocity of 13888.8 m/s
      \(s_d=\cfrac{2000}{100}\left[(5\times 10^5-482)+482\times \ln\left(\cfrac{482}{5\times 10^5}\right)\right]\) [From results obtained at (b)]
      \(=9923415.8 \, m\)
      
      Time taken by rocket to travel distance of \(0.1 \mathrm{AU}=\cfrac{M-m}{\dot{m}}+\cfrac{0.1 \mathrm{AU}-s_d}{v_f}\)
      \(=\cfrac{5\times 10^5-482}{100}+\cfrac{0.1 \times 1.5 \times 10^{11}-9923415.8}{13888.8}\)
      \(=1084287.6 \, s = 12.55\) days
      
      
2. Season Phenomenon
   Have you ever wondered why summer is too hot and winter is too cold? Earth is always almost at a same distance from the sun whether its summer or winter. Tilting of earth is enough to produce this huge difference. Let's see how.
   
   
   1. The average surface temperature of sun is \(6000 K .\) Use Stefan-Boltzmann law to find the amount of heat energy radiated by sun per second. [Radius of sun \(=696,340 \mathrm{km}\), Stefan's constant \(\sigma=5.67 \times 10^{-8} \mathrm{Wm}^{-2} \mathrm{K}^{-4}\)]
      
      Solution:
      Heat energy radiated by sun per second \(=\sigma AT^4\)
      \(H_{\text{Sun}}=(5.67\times 10^{-8}) \times (4 \pi \times 696340000^2) \times 6000^4\)
      \(=4.477 \times 10^26\) J/s
      
      
   2. The earth is located \(1 A U=1.5 \times 10^{8} \mathrm{km}\) far from sun. Calculate the amount of heat energy received per unit time by a unit normal surface at a distance \(1 A U\) from the sun.
      
      Solution:
      Heat Received by a unit normal surface at a distance \(1 AU\) from the sun \(=\cfrac{H_s}{4 \pi r^2}\)
      \(H_n=\cfrac{4.477\times 10^{26}}{4\pi (1.5\times 10^{11})^2}\)
      \(=1583.6\) J/s
      
      
   3. Our country has an area of \(147,181 k m^{2}\) and is situated at a mean latitude of \(28^{\circ} N .\)
      
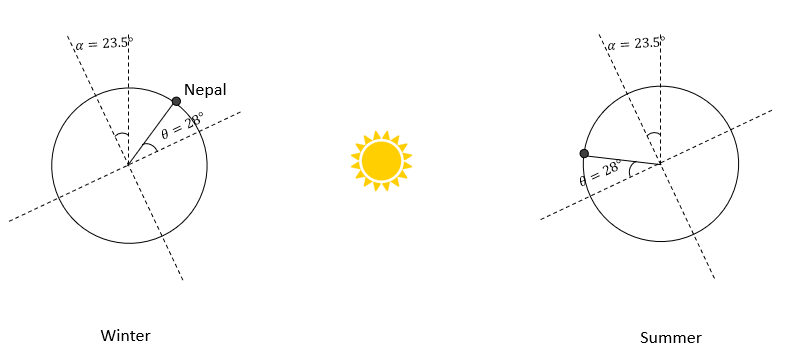
      The Earth has an axial tilt of \(\alpha=23.5^{\circ} .\) Calculate the amount of energy received by Nepal per second in summer and winter at noon accounting the orientation of area.
      
      Solution: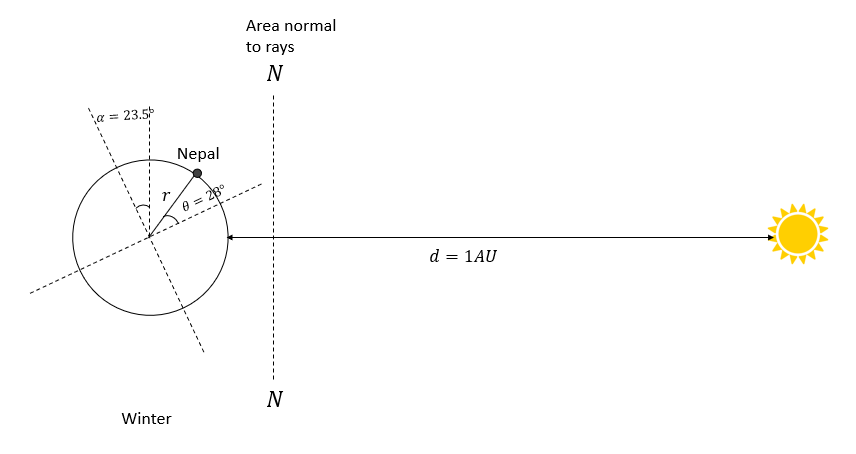
      
      Accounting the fact \(r<<d\), we neglect the effect of \(r\) in distances. The area normal to the rays of light is shown by the line N-N in the above projection.
      Projecting the area of Nepal on N-N during both season, we can calculate the amount of heat received by the country.
      
      In winter, Heat received by Nepal \(H_w=147181 \times 10^6 \times \cos(23.5+28) \times H_n\)
      \(=1.451 \times 10^{14}\) J/s
      
      in summer, Heat received by Nepal \(H_s=147181 \times 10^6 \times \cos(28-23.5) \times H_n\)
      \(=2.324 \times 10^{14}\) J/s
      
      
   4. Calculate the surface temperature of Nepal at noon in both seasons considering heat received is equal to heat lost by radiation at that temperature. For heat loss use the formula \(H_{l}=c \sigma A T_{s}^{4}\) where \(c\) is the correction factor, \(c=2.5\) and \(T_{s}\) is surface temperature.
      
      Solution:
      Nepal's temperature in winter \(T_s=\sqrt[4]{\cfrac{H_w}{c\sigma A}}\)
      \(=\sqrt[4]{\cfrac{1.451 \times 10^{14}}{2.5 \times (5.67\times 10^{-8}) \times (147181\times 10^6)}}\)
      \(=288.8 \, K = 15.8 ^{\circ}C\)
      
      Nepal's temperature in summer \(T_s=\sqrt[4]{\cfrac{H_w}{c\sigma A}}\)
      \(=\sqrt[4]{\cfrac{2.324 \times 10^{14}}{2.5 \times (5.67\times 10^{-8}) \times (147181\times 10^6)}}\)
      \(=324.9 \, K = 51.9 ^{\circ}C\)
      
      
3. Rainbow Physics
   Rainbow is caused by total internal reflection of sunlight in water droplets. Let us solve to see how.
   
   
   1. A ray of light enters a spherical rain drop with an incident angle \(i\) normal to the surface. The ray gets refracted at \(A\), internally reflected at \(B\) and emerged at \(C\). Find the deflection angle of the ray, \(\delta (i)\) as a function of incidence angle \(i\) and refractive index of water \(\eta\).
      
      
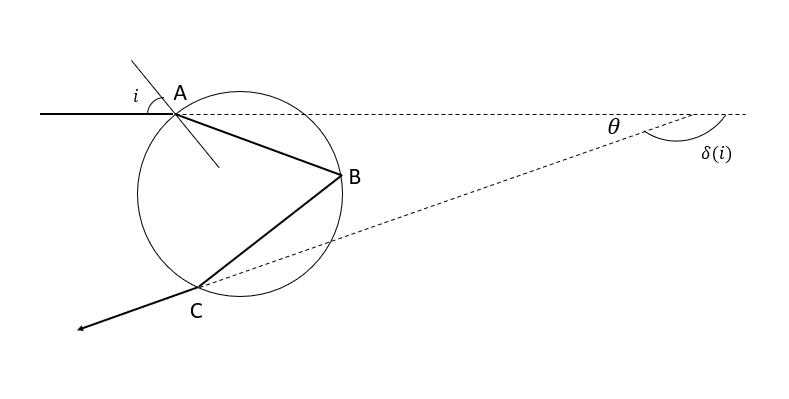
      Solution: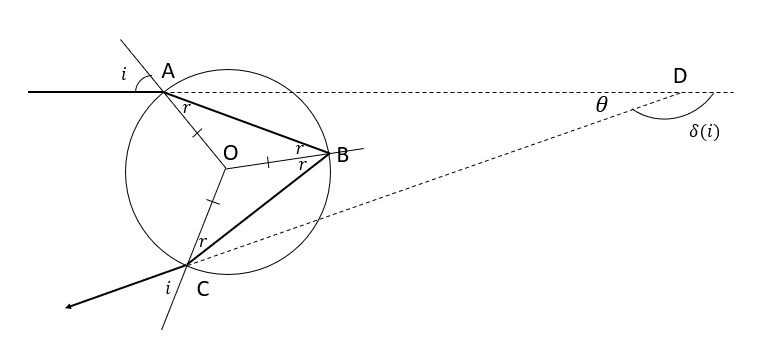
      
      In quadilateral ABCD,
      \(\angle DAB + \angle ABC +\angle BCD + \angle CDA = 360^{\circ}\)
      \(\Rightarrow (i-r)+(360^{\circ}-2r)+(i-r)+(180^{\circ}-\delta(i))=360^{\circ}\)
      \(\Rightarrow \delta (i) = 180 +2i-4r\) .....(i)
      
      From Snell's law of refraction, \(\eta=\cfrac{\sin i}{\sin r}\)
      \(\Rightarrow r=\sin^{-1}\left(\cfrac{\sin i}{\eta}\right)\)
      
      Substituting \(r\) in equation (i),
      \(\delta (i) = 180 +2i-4\sin^{-1}\left(\cfrac{\sin i}{\eta}\right)\)
      
      
      
   2. Maximum dispersion of white light takes place when the deflection angle \(\delta (i)\) is minimum and \(\theta\) in the above figure above is maximum. Find the angle of incidence for which the light is deviated minimum. Also find the angle of minimum deviation \(\delta_m\) and corresponding value of \(\theta_m\). [Take refractive index of water for mean green light \(\eta\) = 1:334]
      
      Solution:
      To find angle of minimum deviation,
      \(\cfrac{d\delta(i)}{di}=0\)
      \(\Rightarrow 2-4\cfrac{1}{\sqrt{1-\left(\cfrac{\sin i}{\eta}\right)^2}}\times \cfrac{\cos i}{\eta}=0\)
      \(\Rightarrow \sqrt{\eta^2-\sin^2 i}=2\cos i\)
      \(\Rightarrow \eta^2=4\cos^2 i+\sin^2 i\)
      \(\Rightarrow i=\cos^{-1}\left(\sqrt{\cfrac{\eta^2-1}{3}}\right)\)
      Taking \(\eta=1.334\) for mean green light,
      \(\therefore i=59.35^{\circ}\)
      
      Also from (a), \(\delta_m=138.07^{\circ}\)
      \(\therefore \theta_m = 180^{\circ}-138.07^{\circ}=41.93^{\circ}\)
      
      
   3. A person is going to observe rainbow. The dispersed rays should make an angle of \(\theta_m\) with the direction of sun's rays. Realizing the three-dimensional world, draw the shape of rainbow as observed by the man taking the above fact into account.
      
      
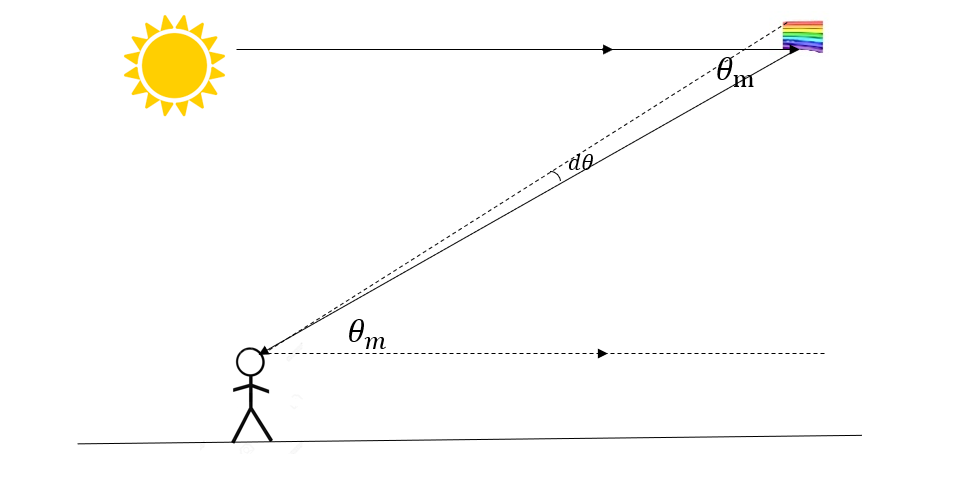
      Solution: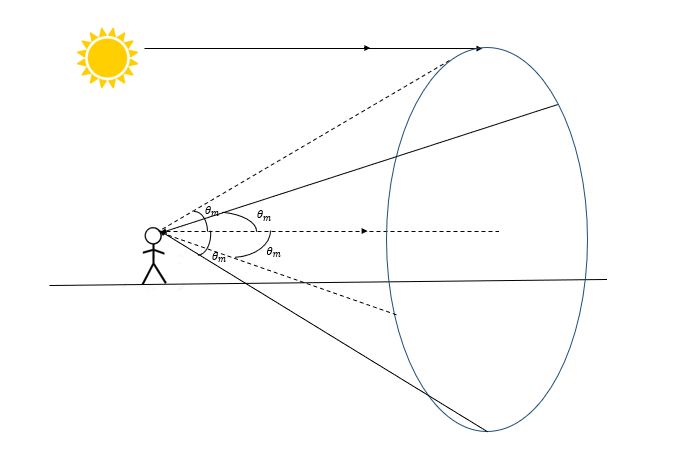
      
      Three dimensional picture of a rainbow is a circle formed at the base of the cone whose semi vertical angle is \(\theta_m=41.93^{\circ}\)
      
      
   4. The refractive index of any material (in this case water) depends upon the wavelength of light as given by Cauchy relation:
      \(\eta(\lambda)=1.3199+\cfrac{6878}{\lambda^{2}}-\cfrac{1.132 \times 10^{9}}{\lambda^{4}}+\cfrac{1.11 \times 10^{14}}{\lambda^{6}}\) where \(\lambda\) is in \(nm\).
      Calculate refractive index of water for red and violet light with wavelength \(\lambda_r = 750 \, nm\) and \(\lambda_v = 350 \, nm\). Use this to find the angular thickness \(d\theta\) of rainbow color band observed by the man with the help of equation obtained in (a).
      
      Solution:
      \(\eta_r=1.3199+\cfrac{6878}{750^{2}}-\cfrac{1.132 \times 10^{9}}{750^{4}}+\cfrac{1.11 \times 10^{14}}{750^{6}}=1.329\)
      \(\eta_v=1.3199+\cfrac{6878}{350^{2}}-\cfrac{1.132 \times 10^{9}}{350^{4}}+\cfrac{1.11 \times 10^{14}}{350^{6}}=1.361\)
      
      From result obtained at (b),
      \(\theta_m=4\times \sin^{-1}\left(\cfrac{\sin\left(\cos^{-1}\left(\sqrt{\cfrac{n^2-1}{3}}\right)\right)}{\eta}\right)-2\times \cos^{-1}\left(\sqrt{\cfrac{n^2-1}{3}}\right)\)
      \(\theta_r=42.66^{\circ}\)
      \(\theta_v=38.17^{\circ}\)
      \(\therefore d\theta=\theta_r-\theta_v=4.49^{\circ}\)